而組頭制最大的問題,其實不是「考前要死命審稿」(不管什麼制,考前一定都會有人審稿),而是組頭的負擔太重。整個學期下來,共筆組員大概要寫五、六次共筆,工作內容是「把老師講的整理出來」,而組頭群平均一個禮拜審一次稿,整個學期審了十三次。工作內容除了聽老師的上課內容外,還要校對組員的稿,還要看原文書補充,如果組頭人數不多,可能每次審稿都要審好幾個組員的稿,一審就是半本共筆。總而言之,組頭工作的次數大概是共筆組員的兩倍,而每次工作的工作量也是組員的兩倍以上,造成組頭負擔太重,這應該是組頭們不想當組頭的原因。
不過我認為,其實這一切應該可以透過正確的人力分配解決。
再把焦點回到互審制,互審制最大的問題,以經濟學角度來說就是分工不當。講個小故事:船長和阿瓜因為船難漂流到小島上,他們靠島上的食物維生。船長每天可以抓80隻魚,獵8隻豬,而笨手笨腳的阿瓜每天只能抓20隻魚,獵4隻豬(請注意:阿瓜兩樣能力都小於船長!),如果兩人每天都用一半的時間抓魚,一半的時間抓豬,那麼他們一天可以得到的收穫是50隻魚和6隻豬。可是如果兩人調整一下:
假如兩人都全力捕魚,那麼他們每天都有100的漁獲量,但是船長抓到的每隻魚,都是用0.1隻豬換來的,而阿瓜抓到的每隻魚,都是用0.2隻豬換來的,聰明的讀者可以發現,假設阿瓜放棄他所有的20隻魚換成4隻豬(每天施展全力抓豬),船長放棄30隻魚換成3隻豬,(每天用八分之五的工作時間抓魚,剩下抓豬)那麼他們每天一樣可以吃到50隻魚,可是可以吃到的豬變成7隻。
這就是機會成本的概念了。
回到共筆制度,假定每次寫稿負擔是a,審稿負擔是b,「減輕壓力」的要件就是:定義一最佳組頭人數n1和寫稿人數n2,使得學期末,每人所做的工作相等,依據簡單的小學術學,令n1:n2 = b:a(成反比)即可。如此一來,組頭制下的組頭和組員都和互審制一樣輕鬆、和原先互審制一樣,而每人負荷又相等,而且有組頭制質量的共筆。
舉例:假定大體實有30堂課,互審制班上90人分30組共筆組,審稿負擔2,寫稿負擔1,那麼互審制一個學期下來每人為共筆付出的心血為3。但是如果改用組頭制,60人審稿,30人寫稿,組頭人數比組員人數為2:1,則每位組頭整學期付出心血:2 * 30堂課 * 每堂課3份稿 / 60個組頭 = 3(注意:每個共筆組被動用3次),寫稿者負擔:1 * 30堂課 * 每堂固定用3個人 / 30個共筆組員 = 3,組頭和審稿人負擔一樣,而且組頭制下平均負擔也和互審制負擔一樣,但是共筆品質變好。
簡而言之,如果某工作是另外一件工作兩倍累,那麼這個工作就用另外一件工作兩倍的人數。
現在開始建立數學模型。
假定學校開n門課,每門課的相對疲累係數分別為a1,a2....,an(定義:在理想品質下,組頭會比組員累幾倍),每門課全學期上課次數分別為b1,b2,....,bn。設每次寫稿負擔為X,則每門課全班全學期寫稿總負擔分別為3b1X,3b2X,....,3bnX(假定每堂課3人寫稿),每門課全班全學期審稿總負擔分別為3a1b1X,3a2b2X,....,3anbnX(假定每次用3個組頭審稿),那麼每門課審稿總負擔:寫稿總負擔為ai:1,1<=i<=n,各科最理想組頭比組員人數為ai:1,1<=i<=n。假定工作分配完以後真正寫共筆不幹組頭的有m個人好了,那麼每科組頭人數就是a1m,a2m,....,anm。且a1m+a2m+.....+anm + m = M(班上總人口),得等式:

比較複雜的,假如第i科每次寫稿一組共筆組有pi個人,寫完後一堂課的稿由qi個組頭負責審稿,則公式改成
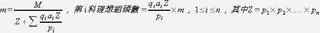
根據此理想化模型,將組頭人數和寫共筆人數按照這個公式分配,就可以在組頭制下讓每個人的終極負擔和在互審制下一樣且全班平均分配。但是仍然可以享受到組頭制的:由比較適合審稿(功課比較好、讀原文能力較佳.....)的人專門審稿,避免考前出現沒責任的人審稿,同一科由同一批人員專門審稿,產生聚集效應....等 全文連結

0 意見:
張貼留言